R Squared Explained: Applications, Limitations, and Improvements

R-squared is a key metric for evaluating the effectiveness of regression models.

This comprehensive guide will walk you through its meaning, calculation, applications, and limitations, empowering you to confidently assess models and make informed decisions based on your data.

What is R-Sq?

R-squared, formally known as the coefficient of determination, is a statistical metric used to gauge the performance of a regression model.

It quantifies the proportion of variance in the dependent variable explained by the independent variables or the predictors included in your model.

R-squared is a valuable tool because:

• It helps you evaluate how well your model explains the observed data.
• It allows you to compare different models and choose the one that best explains the relationship between variables.
• It’s a straightforward way to communicate the predictive power of your model to others.

Mathematical Formula

R-squared is calculated using the following formula:

R-squared = Explained Variation / Total Variation

Detail of formula:

• Explained Variation: This represents the portion of the total variation in the dependent variable that your model accounts for. It’s the difference between the predicted values and the mean of the observed values.
• Total Variation: The overall variation in the dependent variable is calculated as the difference between each observed value and the mean of the observed values.

By dividing the explained variation by the total variation, we get a ratio that expresses the proportion of the variance explained by the model.

Understanding the Range and R-squared Interpretation

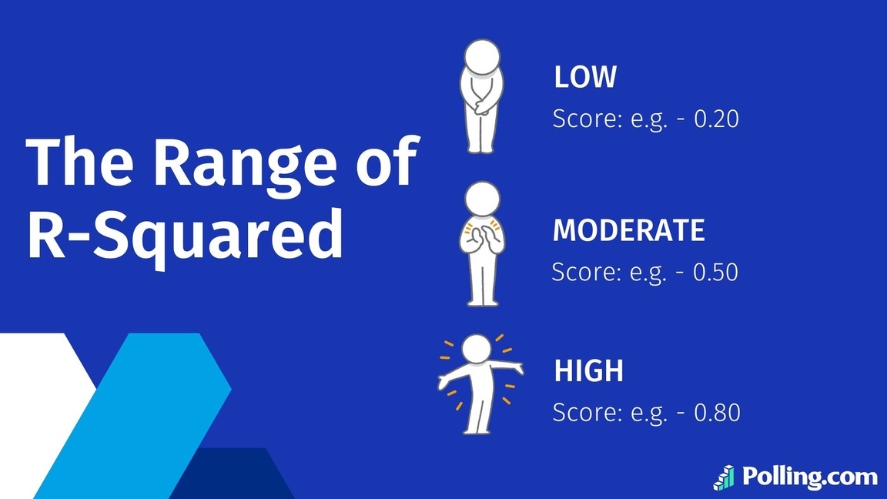
R-squared values always fall within a range of 0 to 1, reflecting how well a model explains the observed data.

• Value of 0: The model has no explanatory power, making predictions no better than random guesses.
• Value of 1: The model perfectly explains the data, though this outcome is extremely rare.

Interpretation Based on Value:

• Low (e.g., 0.20): Explains minimal variance, suggesting missing variables or weak relationships.
• Moderate (e.g., 0.50): Captures a decent amount of variance but has room for improvement.
• High (e.g., 0.80): Accounts for a substantial portion of variance, indicating a strong relationship and good predictive ability.

It’s essential to remember that a high value doesn’t necessarily mean the model is perfect.

The metric can be artificially inflated by adding more independent variables, even if those variables aren’t truly relevant.

So, assessing the model’s overall significance and considering other factors beyond this single measure is crucial.

Calculation of R-Squared

While software simplifies the process, understanding the manual calculation gives you a deeper grasp of R-squared.

Here are the steps:

1. Gather Your Data: Collect pairs of observed values and predicted values.
2. Calculate Residuals: For each pair, subtract the predicted value from the observed value. This difference is called a residual and represents the error in the model’s prediction.
3. Square the Residuals: Square each residual value.
4. Sum of Squares of Residuals (SSR): Add up all the squared residuals.
5. Calculate the Mean of Observed Values: Determine the average of all your observed values.
6. Total Sum of Squares (SST): For each observed value, subtract the mean, square the result, and sum these values.
7. Calculate Explained Sum of Squares (SSE): Subtract the SSR from the SST. The remaining value is the SSE, representing the variance the model successfully explains.
8. Calculate R-Squared: Finally, divide the SSE by the SST to obtain the coefficient of determination, which indicates how well the model explains the variance in the data.

R-squared with Statistical Software

Thankfully, you don’t have to do all those calculations by hand! Statistical software makes it much more manageable.

Some software includes:

• Excel: Use the RSQ function, providing the ranges of observed and predicted values as arguments.
• R: After fitting a linear regression model, the summary() function displays the coefficient of determination along with other model statistics.
• Python: A fitted model’s score() method directly returns this value.

While software simplifies the calculation, understanding the underlying steps enhances your appreciation of what R-squared represents and improves your ability to interpret its results effectively.

Applications of R-Squared

R-squared is generally used and utilized whenever a statistical analysis is performed.

Their major uses are found in two main fields, as stated below.

Regression Analysis

In regression analysis, R-squared evaluates how well a model explains the relationship between independent and dependent variables.

For models with a single predictor, it indicates the strength of the linear relationship, where higher values suggest a stronger association.

Similarly, in multiple linear regression, this measure quantifies the connection between predictors and outcomes. As expected, higher values reinforce the model’s explanatory power.

Model Evaluation

R-squared is a crucial tool for assessing the goodness-of-fit of predictive models.

It measures how well a model’s predictions align with observed data, where higher values indicate stronger alignment.

Additionally, it helps compare the performance of different models on the same dataset, with higher values signifying better explanatory power.

Limitations of R-Squared

R-squared is an excellent tool. However, it does come with its problems.

Awareness of these shortcomings enables you to use the R-squared results appropriately and prevents you from falling into snares.

Overfitting

A high R-squared can sometimes be deceptive.

If a model is overly complex or has too many predictors, it might fit the training data perfectly but fail to generalize to new data. This phenomenon is known as overfitting.

Overfitting can lead to overly optimistic assessments of a model’s predictive power.

A model with a high R-squared on the training data might perform poorly in real-world applications, making inaccurate predictions.

Not Ideal for Non-Linear Relationships

R-squared is inherently designed for linear models, where the relationship between variables is assumed to be straight. So, it may not accurately reflect the model’s performance when dealing with non-linear relationships.

In such cases, one must turn to other measures based on information criteria or cross-validation.

Alternative Metrics

R-squared is not the only metric for evaluating models.

Several alternatives can offer a more holistic view of model performance, including:

• Adjusted R-squared: Accounts for the number of predictors, providing a more reliable comparison between models.
• Root Mean Squared Error (RMSE): Assesses how large the average prediction errors are.
• Mean Absolute Error (MAE): Calculates the average absolute disparity between predicted and actual values.

Thus, by considering these shortcomings and examining other feature versions, anyone can avoid the biases of a single-number measure and contribute to an accurate comparison of their models.

Practical Examples and Case Studies

R-squared finds wide application across diverse fields, aiding professionals in understanding and predicting outcomes.

R-squared in Finance

In finance, this metric is key for portfolio managers, describing how closely a stock’s or fund’s returns align with a benchmark index.

A high value indicates a strong correlation with the market, while a low value suggests more independent movement.

This information is crucial for evaluating risk and diversifying investor portfolios.

For instance, investors may consider a portfolio with a higher value as less diversified since its performance is closely tied to market factors.

R-squared in Healthcare

In the healthcare field, this statistical measure plays a crucial role in reassessing medical remedies.

Specifically, clinical and epidemiological research uses it to evaluate the efficacy of treatment and diagnostic methods. By doing so, researchers can compare different approaches and measure the degree to which various factors influence patient outcomes.

For example, the recovery period or symptoms severity.

Elements of this nature make it possible for healthcare practitioners to quickly ascertain the most likely ways of bringing positive change to their clients.

R-squared in Marketing

Marketers use R-squared when evaluating the effectiveness of advertising campaigns regarding sales, brand recognition, and other performance indicators.

By analyzing the amount of money spent on advertising and the accompanying sales performance, you can determine how strongly sales changes relate to advertising initiatives.

As a result, this insight is useful in guiding marketers to fine-tune their marketing efforts and allocate resources more efficiently.

R-squared in Social Sciences

In social science research, researchers use R-squared to show relationships between various variables, such as socioeconomic status indices and multiple outcomes.

For example, they evaluate how much variation in education levels factors like family income, a parent’s education level, and geographical area can explain.

These findings may be beneficial for directing policy agendas and social interventions to increase learning possibilities.

Case Study

Let’s consider a real estate scenario.

A realtor aims to develop a model to estimate house prices based on size, number of rooms, and location. To achieve this, they gather data and construct a multiple linear regression model based on existing literature.

As a result, they find an R-squared of 0.75. In other words, the chosen factors in the model explain 75% of the variation in house prices. Meanwhile, factors not included in the model, such as house age or condition, may cause the remaining 25%.

Consequently, this model indicates how house prices can be estimated and what aspects define value in the market, even though it is not perfect.

Ultimately, the realtor can use this model to propose suitable home prices to clients and advise on property investments. However, it is essential to consider the model’s limitations, since other factors can also impact the final results.

Conclusion

R-squared is a significant statistical measure that helps assess how effectively a regression model explains the variance in data.

Furthermore, it allows for checking the goodness of fit for the model, comparing two or more models, and determining the closeness of the linkage between variables.

However, while R-squared is a useful tool, it is crucial to consider its limitations.

Therefore, after learning what R-squared is, you should also explore additional parameters like adjusted R-squared, RMSE, and MAE to fully understand your model’s performance.